Índice de contenidos
Importancia del interés compuesto
El post de hoy, sobre la importancia del interés compuesto y simple, es uno de los pilares de la economía, materia que ninguna persona debiera desconocer. Así pues, este conocimiento será la base de cualquier operación financiera, de financiación o de inversión.
Interés Simple
Para empezar definiremos el interés simple. Este es el porcentaje de beneficio que logra el prestatario/inversor anualmente (u otro periodo temporal establecido) a cambio de su dinero.
Por ejemplo en la bolsa de valores las empresas reparten beneficios, y parte de estos son en forma de dividendos. El interés sería el % obtenido entre el importe del dividendo y el valor de cada acción.
En el caso de un préstamo este sería el tipo de interés que se paga al prestatario (banco u otra entidad o persona).
Fórmula Interés simple
La fórmula del interés simple es la siguiente:
VF = VA (1+n*i)
- VF = Valor Futuro o Capital Futuro
- VA = Valor Actual o Valor Inicial o Capital inicial
- i = Tasa de interés anual
- n = Periodo de tiempo (en años)
Como el cálculo la diferencia entre los periodos (el tipo de interés) es la suma de una constante, lo que en matemáticas se conoce como diferencia de la progresión, estamos ante un caso de progresión aritmética.
Calculadora interés simple
Calcula tu propio ejemplo con este formulario:
Ejemplo 1 interés simple
Pido al banco 5.000€ mediante un préstamo a 4 años y una tipo (TAE*) del 8%.
VF = 5.000€ (1+4*8%) = 6.600€ es decir, al final del plazo habré devuelto 6.600€ (5.000 de principal y 1.900 de intereses).
*TAE: Tasa anual equivalente. Es el % de tipo de interés anual promedio una vez incluidos todos los costes y comisiones de la operación.
Ejemplo 2 interés simple
Tengo 215 acciones de REPSOL. Cotiza actualmente a 14€ por acción, con lo que el valor de mi cartera es de 3.010€. La semana que viene reparte dividendos 0,6€/acción, con lo que percibiré 129€. Calcularé el interés de esta operación con un periodo de inversión de 1 año.
3.010 + 129 = 3.010€ (1+1*i)
3.139 /3.010 = 1+i
i = 1,0429 -1 = 0,429 esto es 4,29%
Interés Compuesto
La principal diferencia del interés compuesto respecto del simple es que en el primero reinvertimos los intereses obtenidos (típicamente anual).
Esta reinversión de los nuevos intereses genera un efecto bola de nieve, que hace que conforme pase el tiempo el capital final sea cada vez más grande.
Fórmula del Interés compuesto
La fórmula de interés compuesto es la siguiente:
VF = VA (1+i)n
- VF = Valor Futuro o Capital Futuro
- VA = Valor Actual o Valor inicial o Capital inicial
- i = Tasa de interés anual
- n = Periodo de tiempo (en años)
En el interés compuesto la secuencia de números (para calcular distintas anualidades) se obtiene de multiplicar la misma cantidad, lo que se conoce como progresión geométrica.
Calculadora interés compuesto
Haz tus propios cálculos:
Ejemplo 3 interés compuesto
Tengo un depósito de 10.000€ por el que me dan un interés del 1% al año. Veamos que pasa al cabo de 5 años.
VF = 10.000 (1+1%)5 = 10.510,10€
Manualmente (sin la fórmula) esto lo calcularíamos como:
| Principal | Intereses generados | Total |
| 10.000,00€ | 100,00€ | 10.100,00€ |
| 10.100,00€ | 101,00€ | 10.201,00€ |
| 10.201,00€ | 102,01€ | 10.303,01€ |
| 10.303,01€ | 103,03€ | 10.406,04€ |
| 10.406,04€ | 104,06€ | 10.510,10€ |
Vemos que cada año se incrementan un poco los intereses generados, debido a que obtenemos intereses de los intereses. Si el tipo de interés fuera mayor, veríamos un incremente notable en la cifras. Lo veremos en el ejemplo siguiente.
Ejemplo 4 interés compuesto
Tenemos 10.000€ invertidos en una plataforma de crowfunding (micropréstamos online) que nos da un interés promedio del 10%. Reinvertiremos los beneficios y mantendremos esta operación durante 5 años.
VF = 10.000 (1+10%)5 = 16.105,10€
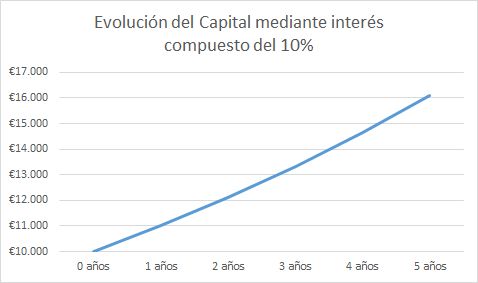
Vemos que en este segundo ejemplo se aprecia una notable mejora de los resultados obtenidos, gracias al buen interés ofrecido.
Diferencias entre interés simple y compuesto
A nivel teórico tal y como hemos visto el interés compuesto es un progresión geométrica mientras que el interés simple es una progresión aritmética. Esto es debido a que en el interés compuesto se reinvierten los intereses, mientras que en el simple no.
A efectos prácticos esto se traduce en una rentabilidad mayor del interés compuesto, como veremos seguidamente.
Comparativa interés simple Vs interés compuesto
Veamos un ejemplo práctico comparando la evaluación del ahorro en los casos del interés simple y el compuesto. Cogemos tres importes iniciales distintos, de 10, 30 y 50 mil euros y vemos su evolución con el tiempo considerando un interés (rendimiento) del 5%. Este rendimiento se podría obtener fácilmente con acciones de la bolsa de valores o mediante un buen fondo de inversión.
Ambos intereses los podemos calcular rápidamente en una hoja de cálculo sin ni siquiera tener que aplicar las fórmulas.
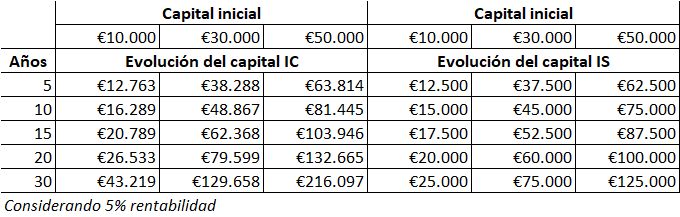
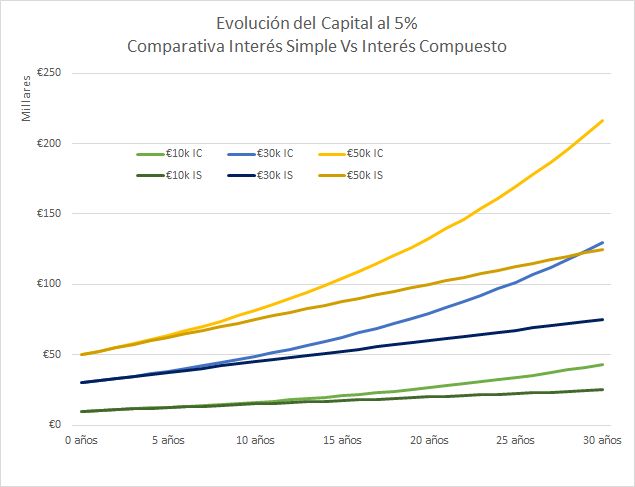
Vemos como conforme pasa el tiempo la rentabilidad obtenida con los dos sistemas diverge progresivamente. El interés compuesto en este caso resulta:
- Un 9% más rentable a los 10 años
- Un 19% más rentable a los 15 años
- Un 33% más rentable a los 20 años
- Un 73% más rentable a los 30 años
Por aclarar la explicación, obviamente esta rentabilidad extra es a costa de renunciar en el momento actual del disfrute de los intereses para recoger estos frutos en el largo plazo. Cada quien luego se tendrá que adaptar a su situación personal. Pero lo importante es tener el concepto teóricamente claro.
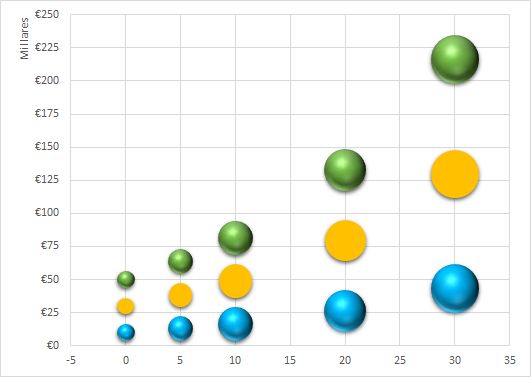
Conclusiones interés simple y compuesto
Como conclusión hemos observado que el interés compuesto supone una rentabilidad extra considerable al compararlo con el interés simple.
Las conclusiones observadas son:

